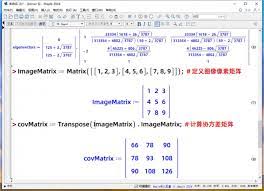
矩阵运算在数学领域里具有举足轻重的意义。作为一款功能强大的数学软件,Maple为我们提供了一种简单且高效的方式来处理矩阵运算。以下将通过几个实用例子详细说明Maple在方形矩阵计算中的应用。
创建矩阵
要利用Maple进行矩阵运算,最基础的一步是创建矩阵。例如,我们创建一个3x3矩阵a:
```
a := matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]);
```
如此便定义了矩阵a的各个元素。
矩阵加法
假设存在另一个3x3矩阵b:
```
b := matrix([[9, 8, 7], [6, 5, 4], [3, 2, 1]]);
```
要计算矩阵a与b的和,只需输入:
```
a + b;
```
Maple会快速地返回结果:
```
matrix([[10, 10, 10], [10, 10, 10], [10, 10, 10]])
```
矩阵乘法
矩阵乘法也是常见的操作。计算矩阵a与b的积:
```
a &* b;
```
Maple将根据矩阵乘法的规则进行计算并输出结果:
```
matrix([[30, 24, 18], [84, 69, 54], [138, 114, 90]])
```
矩阵转置
计算矩阵a的转置:
```
transpose(a);
```
得到的结果是:
```
matrix([[1, 4, 7], [2, 5, 8], [3, 6, 9]])
```
行列式求解
计算矩阵a的行列式:
```
det(a);
```
结果为:
```
0
```
矩阵逆
如果矩阵a有逆,计算其逆矩阵:
```
linearalgebra:-inverse(a);
```
在此例中,因为矩阵a的行列式为0,它不可逆,Maple会提示相应的信息。
通过这些范例,我们能看到Maple在方形矩阵计算方面的显著优势。无论是基本的矩阵操作,还是更复杂的行列式或逆求解等运算,Maple都能准确、高效地给出结果,为数学研究及实际应用中的矩阵运算提供了极大便利。